this post was submitted on 09 Oct 2023
574 points (97.8% liked)
Technology
69867 readers
2865 users here now
This is a most excellent place for technology news and articles.
Our Rules
- Follow the lemmy.world rules.
- Only tech related news or articles.
- Be excellent to each other!
- Mod approved content bots can post up to 10 articles per day.
- Threads asking for personal tech support may be deleted.
- Politics threads may be removed.
- No memes allowed as posts, OK to post as comments.
- Only approved bots from the list below, this includes using AI responses and summaries. To ask if your bot can be added please contact a mod.
- Check for duplicates before posting, duplicates may be removed
- Accounts 7 days and younger will have their posts automatically removed.
Approved Bots
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
EXPLAIN!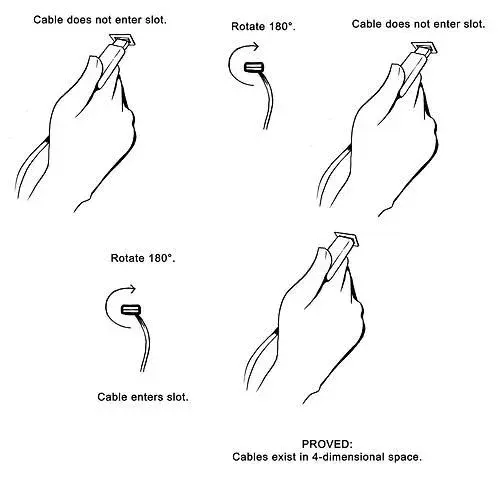
The picture explains itself. The cable exists in a 4-dimensional space.
The reply is pretty self-explanatory too. The cable exists in a 4-dimensional space.
You guys joke about this, but he managed to create a connector with three sides: up, down, and "oh yeah the first side was the correct one"
It doesn't necessarily need to be 4-dimensional https://en.m.wikipedia.org/wiki/Spinor
That entry needs a ELI.
"In geometry and physics, spinors /spɪnər/ are elements of a complex number-based vector space that can be associated with Euclidean space.[b] A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation,[c] but unlike geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms)."
Seems pretty self-explanatory to me! /s
USB-A is a spin-half connector type
Purged by creator