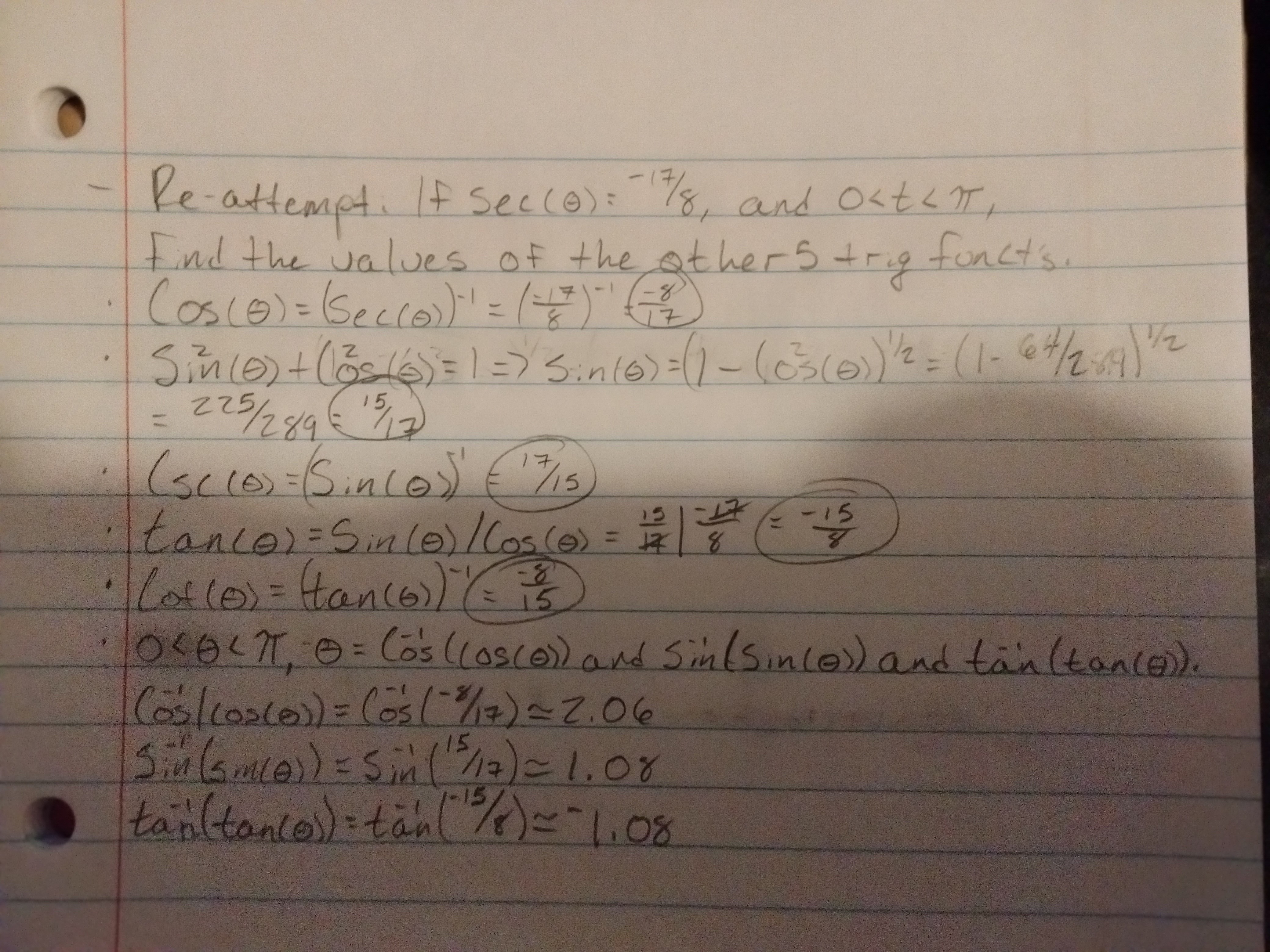The correct answer it the 2.06 from the cosine, but with the sine you're just getting the first quadrant answer, since it's simmetrical.
A place for everything about math
That's definitely insightful- I found pi-arccos=arcsin. So is this a case where the range of arcsin is restricted to q1 and q4, while arccos is restricted to q1 and q2 so can give answers in q2? And why would arctan give the negative of arcsin?
I can tell I'm not quite understanding some fundamental concept, but I can't tell where to focus my review or if I just straight missed something.
Well basically yes you got it, since sin and cos repeat, you can't actually calculate the inverse for any angle, so the domain of the inverse functions is restricted to a range where they are bijective. But simply put, think it on the circle, can the height (sin) tell you if you are left (q2) or right (q1) ? No, but the x coordinate (cos) can :)
Okay thanks. One more question: Unless quadrant is known beforehand (as in this case it was given), is there any way to tell which inverse function is "correct?"
Edit2: Oh, of course- you already said and I already read but forgot: It's based on cos and sine, whether they're negative.
The correct answer is the 2.06 from the cosine, but with the sine you're just getting the first quadrant answer, since it's simmetrical.
not sure if it may help, but maybe check out the graphs at the bottom of the basic concepts section here:
https://en.m.wikipedia.org/wiki/Inverse_trigonometric_functions